Questões de Estatística - Teorema Central do Limite e Lei dos Grandes Números

Questão: 1 de 11

404779

Banca: FGV

Órgão: TJ/RO

Cargo(s): Estatístico

Ano: 2015

Matéria/Assunto: Estatística > Estatística avançada / Teorema Central do Limite e Lei dos Grandes Números

convergência quase certa;

convergência em probabilidade;

convergência em distribuição;

probabilidade condicional;

máxima verossimilhança.

Questão: 2 de 11

340734

Banca: CESPE / Cebraspe

Órgão: TJ/RO

Cargo(s): Analista Judiciário - Estatística

Ano: 2012

Matéria/Assunto: Estatística > Estatística avançada / Teorema Central do Limite e Lei dos Grandes Números

princípio da invariância.

lei fraca dos grandes números.

desigualdade de Chebyshev.

lei forte dos grandes números.

teorema limite central.

Questão: 3 de 11

336503

Banca: CESPE / Cebraspe

Órgão: FUB

Cargo(s): Estatístico

Ano: 2015

Matéria/Assunto: Estatística > Estatística avançada / Teorema Central do Limite e Lei dos Grandes Números

Considerando que, em n ensaios independentes de Bernoulli, a
probabilidade de sucesso de cada um deles seja igual a p, e que X
represente o número de sucessos observados nesses n ensaios,
julgue o item subsecutivo, relativo à lei dos grandes números.

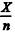Segundo a lei forte dos grandes números, à medida que o tamanho da amostra aumenta, a estatística

converge para uma distribuição normal com média p.

Certo

Errado

Questão: 4 de 11

336507

Banca: CESPE / Cebraspe

Órgão: FUB

Cargo(s): Estatístico

Ano: 2015

Matéria/Assunto: Estatística > Estatística avançada / Teorema Central do Limite e Lei dos Grandes Números

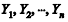
Uma amostra aleatória simples com reposição

foi retirada de uma grande população de alunos do ensino médio
para avaliar suas expectativas acerca do ensino superior. Nessa
amostra,

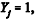se o estudante j já se decidiu acerca de sua carreira
profissional, e

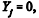se o estudante j ainda não se decidiu sobre
esse assunto.

Com relação ao total amostral, julgue os itens a seguir,
considerando que e que

De acordo com o Teorema Limite Central, S_n é um estimador não viciado da média populacional. Segundo esse teorema,

Certo

Errado

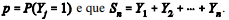
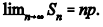
Questão: 5 de 11

290547

Banca: FGV

Órgão: DPE/RJ

Cargo(s): Técnico Superior Especializado - Estatística

Ano: 2019

Matéria/Assunto: Estatística > Estatística avançada / Teorema Central do Limite e Lei dos Grandes Números

na convergência quase certa o limite da probabilidade é nulo;

na convergência quase certa a probabilidade do limite é 1;

na convergência em probabilidade é possível demonstrar que a probabilidade clássica aproxima-se da frequencial;

se X_n converge em distribuição para X e Y_n converge em distribuição para Y (constante real), então a sequência X_n.Y_n converge em distribuição para X.Y.