Logo Mapa da Prova

Questões de Matemática básica

    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado

Limpar pesquisa

Configurar questões
Tamanho do Texto
Modo escuro

Questão: 556 de 19653

296519

copy

Banca: CESPE / Cebraspe

Órgão: Pref. São Cristóvão/SE

Cargo(s): Professor - Matemática

Ano: 2019

Matéria/Assunto: Matemática > Matemática básica / Números / Números reais

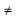Julgue os próximos itens, relativos a funções exponenciais.
Para a > 0 e a1, a função f(x) = 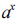pode também ser expressa
como .

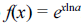Questão: 557 de 19653

296268

copy

Banca: CESPE / Cebraspe

Órgão: Pref. São Cristóvão/SE

Cargo(s): Professor - Matemática

Ano: 2019

Matéria/Assunto: Matemática > Matemática básica / Números / Números reais

Considerando as propriedades e as operações fundamentais dos
números inteiros, racionais, irracionais e reais, julgue os itens a
seguir.
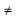Se a, b e c forem números reais tais que 2a² – ab + 3ac 0,
então
.

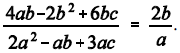
Questão: 558 de 19653

297605

copy

Banca: CESPE / Cebraspe

Órgão: Pref. São Cristóvão/SE

Cargo(s): Professor - Matemática

Ano: 2019

Matéria/Assunto: Matemática > Matemática básica / Números / Números Inteiros

Considerando as propriedades e as operações fundamentais dos
números inteiros, racionais, irracionais e reais, julgue os itens a
seguir.
No conjunto dos números inteiros, o algoritmo da divisão
garante que, dados os números inteiros a e b, com a 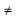0,
existem números inteiros q e r tais que b = q × a + r e 0 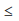r < |a|. O número q é o quociente e r é o resto da divisão
de b por a. Já no conjunto dos números racionais, dados x e y,
com x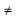0, é sempre possível encontrar um número racional z
tal que y = x × z, isto é, o resto da divisão de y por x seja igual
a zero.

Questão: 559 de 19653

297897

copy

Banca: CESPE / Cebraspe

Órgão: Pref. São Cristóvão/SE

Cargo(s): Professor - Matemática

Ano: 2019

Matéria/Assunto: Matemática > Matemática básica / Números / Números reais

Considerando as propriedades e as operações fundamentais dos
números inteiros, racionais, irracionais e reais, julgue os itens a
seguir.
O produto de dois números racionais é sempre um número
racional. O mesmo é válido para números irracionais: o
produto de dois números irracionais é sempre um número
irracional.

Questão: 560 de 19653

297659

copy

Banca: CESPE / Cebraspe

Órgão: IF/RJ - Fluminense

Cargo(s): Professor - Matemática

Ano: 2018

Matéria/Assunto: Matemática > Matemática básica / Números / Números reais

[ 2, 0)∪(6, 8].

( ∞, 0)∪(6, +∞).

( ∞, 2]∪(6, 8].

[ 2, 8].

(6, +∞).