Questões de Matemática - Algebra Linear - Professor - Matemática - 2008
Limpar pesquisa
Questão: 1 de 6
94208

Banca: CESPE / Cebraspe
Órgão: SEDUC/ES
Cargo(s): Professor - Matemática
Ano: 2008
Matéria/Assunto: Matemática > Matemática superior / Algebra Linear
instituído em substituição à Taxa Rodoviária Única (TRU),
cobrada anualmente no licenciamento dos veículos. A tabela
abaixo mostra, hipoteticamente, valores do IPVA, a serem pagos
em 2008, para alguns veículos de acordo com ano de fabricação
e marca.
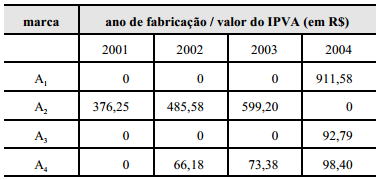
Considere a matriz M, 4 × 4, em que o elemento da i-ésima linha
e j-ésima coluna é o valor do IPVA a ser recolhido pelo
iproprietário do veículo de marca Ai fabricado no ano 200j.
Com base nessas informações, julgue os itens a seguir.
Questão: 2 de 6
92172

Banca: CESPE / Cebraspe
Órgão: SEPLAG/DFT
Cargo(s): Professor - Matemática
Ano: 2008
Matéria/Assunto: Matemática > Matemática superior / Algebra Linear
pagou R$ 3,40. Sabendo-se que o preço unitário de cada fruta foi
o mesmo em cada compra, o problema de se determinar o valor
unitário de cada fruta pode ser expresso por meio de um sistema
composto de duas equações lineares e duas incógnitas, que
também pode ser escrito na forma matricial: AX = B, em que
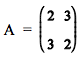 é a matriz dos coeficientes do sistema linear,
é a matriz dos coeficientes do sistema linear, 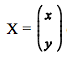 é a matriz das incógnitas e
é a matriz das incógnitas e 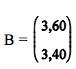 é a matriz dos
é a matriz dostermos independentes.
Com relação a essas informações, julgue os itens seguintes.
 .
.Questão: 3 de 6
92231

Banca: CESPE / Cebraspe
Órgão: SEPLAG/DFT
Cargo(s): Professor - Matemática
Ano: 2008
Matéria/Assunto: Matemática > Matemática superior / Algebra Linear
pagou R$ 3,40. Sabendo-se que o preço unitário de cada fruta foi
o mesmo em cada compra, o problema de se determinar o valor
unitário de cada fruta pode ser expresso por meio de um sistema
composto de duas equações lineares e duas incógnitas, que
também pode ser escrito na forma matricial: AX = B, em que
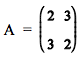 é a matriz dos coeficientes do sistema linear,
é a matriz dos coeficientes do sistema linear, 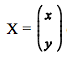 é a matriz das incógnitas e
é a matriz das incógnitas e 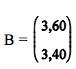 é a matriz dos
é a matriz dostermos independentes.
Com relação a essas informações, julgue os itens seguintes.
Questão: 4 de 6
92266

Banca: CESPE / Cebraspe
Órgão: SEPLAG/DFT
Cargo(s): Professor - Matemática
Ano: 2008
Matéria/Assunto: Matemática > Matemática superior / Algebra Linear
pagou R$ 3,40. Sabendo-se que o preço unitário de cada fruta foi
o mesmo em cada compra, o problema de se determinar o valor
unitário de cada fruta pode ser expresso por meio de um sistema
composto de duas equações lineares e duas incógnitas, que
também pode ser escrito na forma matricial: AX = B, em que
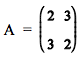 é a matriz dos coeficientes do sistema linear,
é a matriz dos coeficientes do sistema linear, 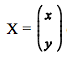 é a matriz das incógnitas e
é a matriz das incógnitas e 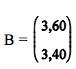 é a matriz dos
é a matriz dostermos independentes.
Com relação a essas informações, julgue os itens seguintes.
Questão: 5 de 6
92282

Banca: CESPE / Cebraspe
Órgão: SEPLAG/DFT
Cargo(s): Professor - Matemática
Ano: 2008
Matéria/Assunto: Matemática > Matemática superior / Algebra Linear
pagou R$ 3,40. Sabendo-se que o preço unitário de cada fruta foi
o mesmo em cada compra, o problema de se determinar o valor
unitário de cada fruta pode ser expresso por meio de um sistema
composto de duas equações lineares e duas incógnitas, que
também pode ser escrito na forma matricial: AX = B, em que
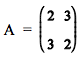 é a matriz dos coeficientes do sistema linear,
é a matriz dos coeficientes do sistema linear, 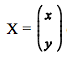 é a matriz das incógnitas e
é a matriz das incógnitas e 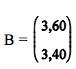 é a matriz dos
é a matriz dostermos independentes.
Com relação a essas informações, julgue os itens seguintes.
 .
.