Questões de CESGRANRIO - Matemática - Geometria Plana

Em uma malha quadriculada composta por 100 quadradinhos idênticos, foi desenhada e pintada uma figura de 5 lados, como se pode ver a seguir.



Assim, verifica-se que a região pintada corresponde a x% de toda a malha.

O valor de x é

Um quadrado foi dividido em 5 retângulos de mesma área, conforme a Figura a seguir:



Da Figura, tem-se ainda que um dos lados do retângulo 5 mede 10 cm.

A área do retângulo 3 vale

Em cada um dos quadrados menores que formam o quadrado da Figura a seguir será colocado um dos números 1, 2 ou 3, de modo que não haja números repetidos na mesma linha nem números repetidos na mesma coluna.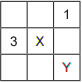



A soma dos números representados pelas letras X e Y da

Figura vale

Ao duplicar a largura de um determinado retângulo e reduzir à metade o comprimento desse mesmo retângulo, obtém-se um quadrado de perímetro P.

O perímetro do retângulo original é

O retângulo ABCD foi dividido em 12 retângulos menores, todos iguais. Em cada um desses retângulos foi traçada uma de suas diagonais, como mostra a Figura abaixo.



A razão entre as áreas do triângulo PQR e do retângulo

ABCD é igual a