Questões de CESGRANRIO - Raciocínio Lógico - Lógica proposicional
Limpar pesquisa
Questão: 21 de 44
101564

Banca: CESGRANRIO
Órgão: Vibra Energia
Cargo(s): Analista de Sistemas Júnior - Ênfase em Infraestrutura
Ano: 2011
Matéria/Assunto: Raciocínio Lógico > Lógica proposicional
RC1 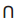
RC1 U RC2 seja consistente.
RC1 → RC2 seja uma tautologia.
RC2 ↔ RC1 seja válido.
RC1 e RC2 sejam logicamente equivalentes.
Questão: 22 de 44
101576

Banca: CESGRANRIO
Órgão: Vibra Energia
Cargo(s): Analista de Sistemas Júnior - Ênfase em Infraestrutura
Ano: 2011
Matéria/Assunto: Raciocínio Lógico > Lógica proposicional
p ∧ ((q ∨ ¬ r) ∧ (¬ q ∨ r)) ∧ s ∧ ¬ t.
¬ p ∧ ((q ∧ ¬ r) ∨ (¬ q ∧ r)) ∧ s ∧ ¬ t.
p ∧ (q ∨ r) ∧ ¬ s ∧ ¬ t.
p ∧ (q ∨ r ∨ ¬ s) ∧ t.
¬ p ∧ ((q ∧ r) ∨ s) ∧ t.
Questão: 23 de 44
101612

Banca: CESGRANRIO
Órgão: Vibra Energia
Cargo(s): Analista de Sistemas Júnior - Ênfase em Telecomunicações
Ano: 2011
Matéria/Assunto: Raciocínio Lógico > Lógica proposicional
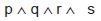
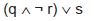
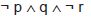
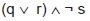
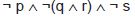
Questão: 24 de 44
101252

Banca: CESGRANRIO
Órgão: Petrobras
Cargo(s): Analista de Sistemas Júnior - Processos de Negócios
Ano: 2012
Matéria/Assunto: Raciocínio Lógico > Lógica proposicional
2.
3.
4.
5.
6.
Questão: 25 de 44
101251

Banca: CESGRANRIO
Órgão: Petrobras
Cargo(s): Analista de Sistemas Júnior - Processos de Negócios
Ano: 2012
Matéria/Assunto: Raciocínio Lógico > Lógica proposicional
Nenhum professor de matemática usa óculos.
Ninguém que usa óculos é professor de matemática.
Todos os professores de Matemática não usam óculos.
Existe alguma pessoa que usa óculos e não é professor de matemática.
Existe algum professor de matemática que não usa óculos.
