Logo Mapa da Prova

Questões de Estatística avançada - Amostragem

    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado

Limpar pesquisa

Configurar questões
Tamanho do Texto
Modo escuro

Questão: 46 de 5032

402708

copy

Banca: FGV

Órgão: MPE/BA

Cargo(s): Analista Técnico - Estatística

Ano: 2017

Matéria/Assunto: Estatística > Estatística avançada / Inferência Estatística

quanto mais intensa for a micronumerosidade, mais precisos serão os estimadores de MQO;

o número de parâmetros de um modelo deve ser sempre superior ao tamanho da amostra disponível para a estimação;

quanto maior o número de parâmetros em uma regressão, menor será a variância estimada dos erros;

se duas variáveis estão provocando a micronumerosidade, ambas devem ser excluídas da equação de regressão;

a micronumerosidade pode não ser um problema sério caso a regressão seja usada para projeções e não para estimações.

Questão: 47 de 5032

404784

copy

Banca: FGV

Órgão: TJ/RO

Cargo(s): Estatístico

Ano: 2015

Matéria/Assunto: Estatística > Estatística avançada / Inferência Estatística

1/256;

3/128;

27/128;

101/128;

125/128.

Questão: 48 de 5032

390700

copy

Banca: IBFC

Órgão: Ebserh

Cargo(s): Analista Administrativo - Estatística

Ano: 2020

Matéria/Assunto: Estatística > Estatística avançada / Controle Estatístico de qualidade

R$ 0,09

R$ 0,10

R$ 0,08

R$ 0,07

R$ 0,12

Questão: 49 de 5032

325964

copy

Banca: CESPE / Cebraspe

Órgão: STM

Cargo(s): Analista Judiciário - Estatística

Ano: 2018

Matéria/Assunto: Estatística > Estatística avançada / Outras distribuições de probabilidade

Supondo que o custo unitário X de um processo de execução fiscal
na justiça federal seja descrito por uma distribuição exponencial
com média igual a R$ 5.000, julgue os próximos itens.
P(X > 5.000 | X > 1.000) < P(X > 5.000).

Questão: 50 de 5032

313953

copy

Banca: CESPE / Cebraspe

Órgão: TJ/AM

Cargo(s): Analista Judiciário - Estatística

Ano: 2019

Matéria/Assunto: Estatística > Estatística avançada / Funções de distribuição e densidade de probabilidade

Em determinado tribunal, a data em que cada processo
é protocolado marca a data inicial deste, a partir da qual é contada
a quantidade de meses que se passam até que o juiz apresente
a decisão final sobre ele. Essa quantidade de meses é uma variável
aleatória X cuja função densidade de probabilidade é dada
por 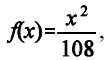, para 0 < x 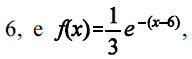, para x > 6,
em que e é o número de Euler, base dos logaritmos neperianos.


A partir dessas informações, julgue os itens a seguir.
Sabendo-se que G(x) = –(x + 1)e–x é primitiva de F(x) = xe–x, conclui-se que, no tribunal em questão, é superior a seis meses o tempo médio esperado até a decisão final para os processos protocolados.