Questões de Estatística - Estatística avançada - Assimetria e Curtose

Em um concurso, a prova de Estatística tem 15 questões, com notas de 0 a 5, de acordo com o número de questões corretas. Sabe-se que as notas têm distribuição normal com média 7,5 e variância de 2,25.

Sabe-se que F(z) é a função de distribuição acumulada da normal padrão, onde 𝐹(1,3) ≅ 0,90, 𝐹(1,64) ≅ 0,95, 𝐹(1,96) ≅ 0,975, 𝐹(2,58) = 0,995

Qual a maior nota entre os 5% que tiraram as menores notas do concurso?

A Administração de uma empresa, fabricante de calculadoras científicas, indica que a quantidade em estoque de suas calculadoras segue uma distribuição normal com média de 1800 unidades e desvio-padrão de 36.


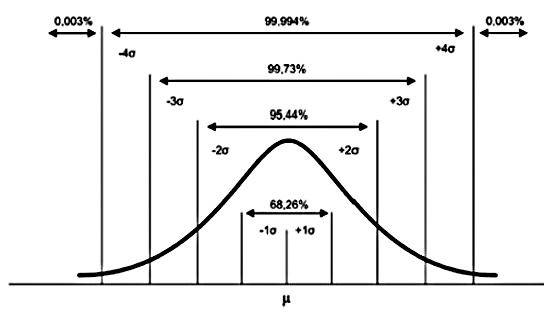
Distribuição normal padrão.

Qual é a probabilidade de, ao se verificar o estoque da empresa, apresentar menos de 1764 unidades?

Uma construtora comprou um grande lote de peças de mármore diretamente de uma grande marmoraria para a construção de casas populares. As peças vêm embaladas de forma individual. Um funcionário da construtora inspeciona cinco peças para verificar o número de peças quebradas ou danificadas. A perda de materiais na construção civil é bastante elevada. Os percentuais de perdas de alguns materiais preocupam as empresas. Sabendo-se que um grande lote contém 1% de peças quebradas ou danificadas, analise as seguintes afirmativas:

I. A probabilidade de o funcionário encontrar no máximo uma peça quebrada ou danificada é 1,04x(0,99)⁴.
II. A probabilidade de o inspetor encontrar pelo menos uma peça quebrada ou danificada é 1 − 0,99⁵.
III. A probabilidade de o inspetor encontrar todas as peças defeituosas é (0,01)²𝑥(0,99)³.

Assinale

Em uma gráfica, uma grande impressora tem sua produção interrompida na primeira ocorrência de um defeito. A impressora tem probabilidade de 10% de apresentar defeito em qualquer dia. Deseja-se planejar um cronograma para limpeza e decidiuse avaliar, probabilisticamente, a espera, até a produção ser interrompida. Seja X, a variável aleatória que conta o número de dias que antecedem a interrupção. Admitindo que os desempenhos, nos sucessivos dias, sejam independentes. Qual a probabilidade de que a interrupção seja no máximo em três dias?

Em um movimentado shopping de uma cidade, um quiosque de venda de pretzels recebe 2 clientes por minuto, e que essa razão seja bem aproximada por um processo de Poisson. Observando a chegada de clientes por 30 segundos, determine a probabilidade de chegar, pelo menos, 3 clientes (caso seja necessário, use o valor de 𝑒⁻¹ = 0,368).