Questões de Matemática - Matemática básica - Números reais
Limpar pesquisa
Questão: 6 de 414
296519

Banca: CESPE / Cebraspe
Órgão: Pref. São Cristóvão/SE
Cargo(s): Professor - Matemática
Ano: 2019
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
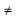 1, a função f(x) =
1, a função f(x) = 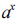 pode também ser expressa
como
pode também ser expressa
como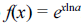 .
.Questão: 7 de 414
296629

Banca: CESPE / Cebraspe
Órgão: Pref. São Cristóvão/SE
Cargo(s): Professor - Matemática
Ano: 2019
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
subsequentes.
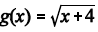 .
.Questão: 8 de 414
296268

Banca: CESPE / Cebraspe
Órgão: Pref. São Cristóvão/SE
Cargo(s): Professor - Matemática
Ano: 2019
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
números inteiros, racionais, irracionais e reais, julgue os itens a
seguir.
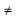 0,
então
0,
então 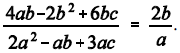 .
.Questão: 9 de 414
297897

Banca: CESPE / Cebraspe
Órgão: Pref. São Cristóvão/SE
Cargo(s): Professor - Matemática
Ano: 2019
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
números inteiros, racionais, irracionais e reais, julgue os itens a
seguir.
Questão: 10 de 414
296555

Banca: CESPE / Cebraspe
Órgão: Pref. São Cristóvão/SE
Cargo(s): Professor - Matemática
Ano: 2019
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
subsequentes.
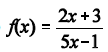 é o conjunto dos números
reais diferentes de 1/5. Nesse conjunto, a função f(x) é bijetiva
e a sua inversa, g(x), é expressa por
é o conjunto dos números
reais diferentes de 1/5. Nesse conjunto, a função f(x) é bijetiva
e a sua inversa, g(x), é expressa por 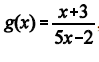 , definida para
todo número real x tal que
, definida para
todo número real x tal que 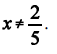 .
.