Questões de Matemática - Matemática básica - Números reais
Limpar pesquisa
Questão: 221 de 369
95457
Banca: FCC
Órgão: METRÔ/SP
Cargo(s): Assistente Administrativo Júnior
Ano: 2012
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
0,925.
0,975.
1,245.
1,455.
1,495.
Questão: 222 de 369
95406
Banca: FCC
Órgão: METRÔ/SP
Cargo(s): Ajudante - Almoxarifado
Ano: 2008
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
–2 e –1.
–1 e 0.
0 e 1.
1 e 2.
2 e 3.
Questão: 223 de 369
95334
Banca: FCC
Órgão: METRÔ/SP
Cargo(s): Almoxarife
Ano: 2010
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
0,0607.
0,607.
6,07.
60,7.
607.
Questão: 224 de 369
94210
Banca: CESPE / Cebraspe
Órgão: SEDUC/ES
Cargo(s): Professor - Matemática
Ano: 2008
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
compreender a matemática por meio de sua história. Determinar
o tamanho do lado de um quadrado cuja área é igual à de um
círculo dado é um problema relacionado ao de se encontrar
valores aproximados para o número B e que mereceu a atenção
de matemáticos desde a antiguidade. Além disso, vários métodos
para se calcular a raiz quadrada de um número são encontrados
na história da matemática.
O método de Heron de Alexandria — 10 d.C a 75 d.C —
permite calcular aproximadamente a raiz quadrada de um número
n = a2 + b por meio da relação
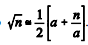. Na Idade Média,calculava-se a raiz quadrada aproximada de um número
n = a2 + b por meio da relação
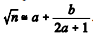.Com base nessas informações e considerando que a2 é o quadrado
perfeito mais próximo de
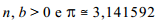, julgue os itensa seguir.
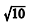obtida aplicando-se o método de Heron fornece uma aproximação para B correta até a 1.ª casa
decimal.Questão: 225 de 369
94240
Banca: CESPE / Cebraspe
Órgão: SEDUC/ES
Cargo(s): Professor - Matemática
Ano: 2008
Matéria/Assunto: Matemática > Matemática básica / Números / Números reais
compreender a matemática por meio de sua história. Determinar
o tamanho do lado de um quadrado cuja área é igual à de um
círculo dado é um problema relacionado ao de se encontrar
valores aproximados para o número B e que mereceu a atenção
de matemáticos desde a antiguidade. Além disso, vários métodos
para se calcular a raiz quadrada de um número são encontrados
na história da matemática.
O método de Heron de Alexandria — 10 d.C a 75 d.C —
permite calcular aproximadamente a raiz quadrada de um número
n = a2 + b por meio da relação
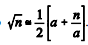. Na Idade Média,calculava-se a raiz quadrada aproximada de um número
n = a2 + b por meio da relação
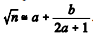.Com base nessas informações e considerando que a2 é o quadrado
perfeito mais próximo de
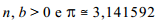, julgue os itensa seguir.
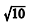obtida aplicando-se a relação
utilizada na Idade Média fornece uma aproximação para B
correta até a 3.ª casa decimal.