Logo Mapa da Prova

Questões de Matemática - Matemática superior - Algebra Linear

    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado

Limpar pesquisa

Configurar questões
Tamanho do Texto
Modo escuro

Questão: 226 de 382

92172

copy

Banca: CESPE / Cebraspe

Órgão: SEPLAG/DFT

Cargo(s): Professor - Matemática

Ano: 2008

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Na compra de duas maçãs e três mangas, uma pessoa pagou R$ 3,60. Outra pessoa comprou três maçãs e duas mangas e
pagou R$ 3,40. Sabendo-se que o preço unitário de cada fruta foi
o mesmo em cada compra, o problema de se determinar o valor
unitário de cada fruta pode ser expresso por meio de um sistema
composto de duas equações lineares e duas incógnitas, que
também pode ser escrito na forma matricial: AX = B, em que 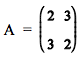é a matriz dos coeficientes do sistema linear, 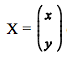é a matriz das incógnitas e 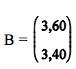é a matriz dos
termos independentes.


Com relação a essas informações, julgue os itens seguintes.
No caso, a inversa da matriz A é a matriz .

Questão: 227 de 382

92266

copy

Banca: CESPE / Cebraspe

Órgão: SEPLAG/DFT

Cargo(s): Professor - Matemática

Ano: 2008

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Na compra de duas maçãs e três mangas, uma pessoa pagou R$ 3,60. Outra pessoa comprou três maçãs e duas mangas e
pagou R$ 3,40. Sabendo-se que o preço unitário de cada fruta foi
o mesmo em cada compra, o problema de se determinar o valor
unitário de cada fruta pode ser expresso por meio de um sistema
composto de duas equações lineares e duas incógnitas, que
também pode ser escrito na forma matricial: AX = B, em que 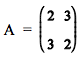é a matriz dos coeficientes do sistema linear, 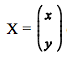é a matriz das incógnitas e 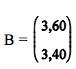é a matriz dos
termos independentes.


Com relação a essas informações, julgue os itens seguintes.
O preço de 4 mangas foi igual a R$ 2,40.

Questão: 228 de 382

92282

copy

Banca: CESPE / Cebraspe

Órgão: SEPLAG/DFT

Cargo(s): Professor - Matemática

Ano: 2008

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Na compra de duas maçãs e três mangas, uma pessoa pagou R$ 3,60. Outra pessoa comprou três maçãs e duas mangas e
pagou R$ 3,40. Sabendo-se que o preço unitário de cada fruta foi
o mesmo em cada compra, o problema de se determinar o valor
unitário de cada fruta pode ser expresso por meio de um sistema
composto de duas equações lineares e duas incógnitas, que
também pode ser escrito na forma matricial: AX = B, em que 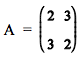é a matriz dos coeficientes do sistema linear, 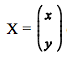é a matriz das incógnitas e 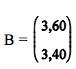é a matriz dos
termos independentes.


Com relação a essas informações, julgue os itens seguintes.
O problema de se determinar o preço unitário de cada fruta se resumiu em resolver o seguinte sistema de equações lineares: .

Questão: 229 de 382

92231

copy

Banca: CESPE / Cebraspe

Órgão: SEPLAG/DFT

Cargo(s): Professor - Matemática

Ano: 2008

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Na compra de duas maçãs e três mangas, uma pessoa pagou R$ 3,60. Outra pessoa comprou três maçãs e duas mangas e
pagou R$ 3,40. Sabendo-se que o preço unitário de cada fruta foi
o mesmo em cada compra, o problema de se determinar o valor
unitário de cada fruta pode ser expresso por meio de um sistema
composto de duas equações lineares e duas incógnitas, que
também pode ser escrito na forma matricial: AX = B, em que 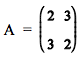é a matriz dos coeficientes do sistema linear, 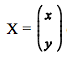é a matriz das incógnitas e 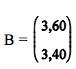é a matriz dos
termos independentes.


Com relação a essas informações, julgue os itens seguintes.
 Para obter o preço unitário de cada fruta, é suficiente multiplicar a inversa da matriz A à esquerda da matriz B.

Questão: 230 de 382

90460

copy

Banca: CESPE / Cebraspe

Órgão: IBAMA

Cargo(s): Analista Ambiental - Monitoramento, regulação, controle, fiscalização e auditoria ambiental

Ano: 2012

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Julgue os itens subsequentes, relacionados a problemas aritméticos,
geométricos e matriciais.
Considere que A e B sejam matrizes distintas, de ordem 2 × 2, com entradas reais e, em cada matriz, três das quatro entradas sejam iguais a zero. Além disso, considere também que A × A = B × B = A × B = O, em que O é a matriz nula, isto é, a matriz em que todas as entradas são iguais a zero. Nesse caso, necessariamente, A = O ou B = O.