Questões de Matemática - Matemática superior

Questão: 346 de 382

463375

Banca: CESPE / Cebraspe

Órgão: Petrobras

Cargo(s): Análise - Comércio e Suprimento

Ano: 2022

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Uma forma de analisar uma economia em setores é por meio do modelo de Leontief. Esse modelo pode ser escrito na forma do sistema linear

(I - C)x = d_e ,

em que C é uma matriz quadrada chamada de matriz de d_e consumo, é chamado de vetor de demanda externa e o vetor x corresponde à quantidade produzida de produtos nessa economia.

Considerando uma matriz de consumo

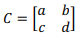
e um vetor de demanda externa d_e = [e f ]^T, ambos com entradas positivas, julgue o item a seguir relacionado ao modelo econômico de Leontief.

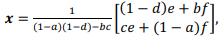
A quantidade x a ser produzida para atender a demanda externa d_e é dada por

contanto que (1 - a) (1 - d ) - bc ≠ 0.

Certo

Errado

Questão: 347 de 382

463376

Banca: CESPE / Cebraspe

Órgão: Petrobras

Cargo(s): Análise - Comércio e Suprimento

Ano: 2022

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Uma forma de analisar uma economia em setores é por meio do modelo de Leontief. Esse modelo pode ser escrito na forma do sistema linear

(I - C)x = d_e ,

em que C é uma matriz quadrada chamada de matriz de d_e consumo, é chamado de vetor de demanda externa e o vetor x corresponde à quantidade produzida de produtos nessa economia.

Considerando uma matriz de consumo

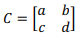
e um vetor de demanda externa d_e = [e f ]^T, ambos com entradas positivas, julgue o item a seguir relacionado ao modelo econômico de Leontief.

Se a soma das entradas de cada uma das colunas de C for menor que 1, então a matriz I - C será inversível.

Certo

Errado

Questão: 348 de 382

447838

Banca: Exatus

Órgão: CERON/RO

Cargo(s): Serviço Social

Ano: 2016

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

x = 1 , y = -1 , z = 3.

x = 2 , y = -2 , z = 3.

x = -2 , y = 2 , z = 1.

x = 1 , y = -1 , z = 2.

Questão: 349 de 382

447787

Banca: Exatus

Órgão: Pref. Caxias do Sul/RS

Cargo(s): Eletricista

Ano: 2018

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Sistema primário divisível, Sistema primário indivisível e Sistema impossível.

Sistema primitivo divisível, Sistema primitivo e Sistema impossível.

Sistema possível e determinado, Sistema possível e indeterminado e Sistema impossível.

Nenhuma das respostas anteriores.

Questão: 350 de 382

447788

Banca: Exatus

Órgão: Pref. Caxias do Sul/RS

Cargo(s): Eletricista

Ano: 2018

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Questões de Matemática - Matemática superior - Algebra Linear