Logo Mapa da Prova

Questões de Matemática - Matemática superior - Algebra Linear

    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado
    Nenhum resultado

Limpar pesquisa

Configurar questões
Tamanho do Texto
Modo escuro

Questão: 376 de 382

424644

copy

Banca: CESPE / Cebraspe

Órgão: SEDUC/AL

Cargo(s): Professor - Matemática

Ano: 2021

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

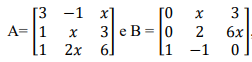Considerando as matrizes A e B com coeficientes reais dadas por , julgue os itens a seguir.
Se x = 0, então a matriz B é invertível e det(B-1) = 1/6.

Questão: 377 de 382

424645

copy

Banca: CESPE / Cebraspe

Órgão: SEDUC/AL

Cargo(s): Professor - Matemática

Ano: 2021

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

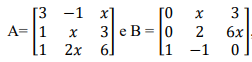Considerando as matrizes A e B com coeficientes reais dadas por , julgue os itens a seguir.
Se det(AB) = 0, então o módulo de x é igual a 1, isto é, |x| = 1.

Questão: 378 de 382

424647

copy

Banca: CESPE / Cebraspe

Órgão: SEDUC/AL

Cargo(s): Professor - Matemática

Ano: 2021

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

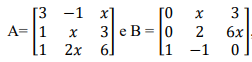Considerando as matrizes A e B com coeficientes reais dadas por , julgue os itens a seguir.
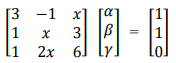O sistema linear dado por tem solução para qualquer valor real de x.

Questão: 379 de 382

424618

copy

Banca: CESPE / Cebraspe

Órgão: SEDUC/AL

Cargo(s): Professor - Matemática

Ano: 2021

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

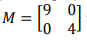Com relação a matrizes e sistemas lineares, julgue os itens a seguir.
Considere que uma matriz quadrada 𝑅 seja a raiz quadrada de uma matriz 𝑀, de mesma dimensão, que satisfaça a equação matricial 𝑅𝑅 = 𝑀. Nesse caso, a matriz tem infinitas raízes quadradas.

Questão: 380 de 382

424619

copy

Banca: CESPE / Cebraspe

Órgão: SEDUC/AL

Cargo(s): Professor - Matemática

Ano: 2021

Matéria/Assunto: Matemática > Matemática superior / Algebra Linear

Com relação a matrizes e sistemas lineares, julgue os itens a seguir.
Considere que 𝐴 seja uma matriz quadrada de dimensão 2, que 𝐼2 seja a matriz identidade, também de dimensão 2, e que 𝑥 ∈ ℝ. Nesse caso, o determinante da matriz 𝑑𝑒𝑡(𝐴 − 𝑥𝐼2 ) = 𝑥² − 𝑡𝑟(𝐴)𝑥 + 𝑑𝑒𝑡(𝐴).