Questões de Matemática - Números complexos

Questão: 46 de 68

5ecbc275f92ea10556087d2a

Banca: CESPE / Cebraspe

Órgão: Secretaria de Estado da Educação de Alagoas

Cargo(s): Professor - Matemática

Ano: 2018

Matéria/Assunto: Matemática > Matemática básica > Números > Números complexos

A respeito dos números complexos, julgue os itens a seguir.

Se n for um número par e se p for um número real diferente de zero, então o polinômio zⁿ + p = 0 tem, necessariamente, duas raízes reais distintas.

Certo

Errado

Questão: 47 de 68

5ecbc275f92ea10556087d34

Banca: CESPE / Cebraspe

Órgão: Secretaria de Estado da Educação de Alagoas

Cargo(s): Professor - Matemática

Ano: 2018

Matéria/Assunto: Matemática > Matemática básica > Números > Números complexos

A respeito dos números complexos, julgue os itens a seguir.

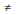Se n > 1 for um número inteiro e se ω Imagem questão

1 for uma raiz n-ésima da unidade (isto é, ωⁿ = 1), então 1 + ω + … + ω^{n - 1} = 0.

Certo

Errado

Questão: 48 de 68

5ecbc276f92ea10556087d3a

Banca: CESPE / Cebraspe

Órgão: Secretaria de Estado da Educação de Alagoas

Cargo(s): Professor - Matemática

Ano: 2018

Matéria/Assunto: Matemática > Matemática básica > Números > Números complexos

A respeito dos números complexos, julgue os itens a seguir.

As raízes do polinômio z³ - 3z² + 3z = 0, no plano complexo, são vértices de um triângulo inscrito no círculo de centro no ponto (1, 0) e de raio 1, isto é, se z = x + iy for uma dessas raízes, então (x - 1)² + y² = 1.

Certo

Errado

Questão: 49 de 68

5ed7f177f92ea119f51aabf7

Banca: CESPE / Cebraspe

Órgão: Prefeitura Municipal de São Cristóvão/SE

Cargo(s): Professor - Matemática

Ano: 2019

Matéria/Assunto: Matemática > Matemática básica > Números > Números complexos

Na disputa entre Cardano e Tartaglia pela resolução da
equação polinomial do terceiro grau (século XVI), foi que se
percebeu que os números reais eram insuficientes para o tratamento
de equações algébricas. Em busca das raízes da equação
x³ - 15x - 4 = 0, a fórmula de Tartaglia fornecia a solução Imagem questão

que evidenciou a necessidade da
criação do conjunto dos números complexos Imagem questão

. Em 1572,
Rafael Bombelli fez a suposição de que Imagem questão

era um número
conhecido e concluiu que Imagem questão

e que

Leonhard Euler (1707-1783) introduziu
a notação Imagem questão

para e passou a estudar os números complexos da
forma z = a + ib, em que a e b são números reais e i² = - 1.

Tendo o texto anterior como referência inicial bem como fatos
históricos da matemática e a teoria dos números complexos, julgue
os itens que se seguem.

Na Grécia Antiga, verificou-se a insuficiência dos números racionais em medir a diagonal do quadrado de lado igual a um.

Certo

Errado

Questão: 50 de 68

5ed7f177f92ea119f51aabff

Banca: CESPE / Cebraspe

Órgão: Prefeitura Municipal de São Cristóvão/SE

Cargo(s): Professor - Matemática

Ano: 2019

Matéria/Assunto: Matemática > Matemática básica > Números > Números complexos

Na disputa entre Cardano e Tartaglia pela resolução da
equação polinomial do terceiro grau (século XVI), foi que se
percebeu que os números reais eram insuficientes para o tratamento
de equações algébricas. Em busca das raízes da equação
x³ - 15x - 4 = 0, a fórmula de Tartaglia fornecia a solução Imagem questão

que evidenciou a necessidade da
criação do conjunto dos números complexos Imagem questão

. Em 1572,
Rafael Bombelli fez a suposição de que Imagem questão

era um número
conhecido e concluiu que Imagem questão

e que

Leonhard Euler (1707-1783) introduziu
a notação Imagem questão

para e passou a estudar os números complexos da
forma z = a + ib, em que a e b são números reais e i² = - 1.

Tendo o texto anterior como referência inicial bem como fatos
históricos da matemática e a teoria dos números complexos, julgue
os itens que se seguem.

O módulo do número z = 2 + i é maior que 2.

Certo

Errado